Overview
这篇博客介绍了扩散模型(Diffusion Model)的整体框架,其中包含了详细的数学推导,希望能够让读者对扩散模型有更加深刻的认识。
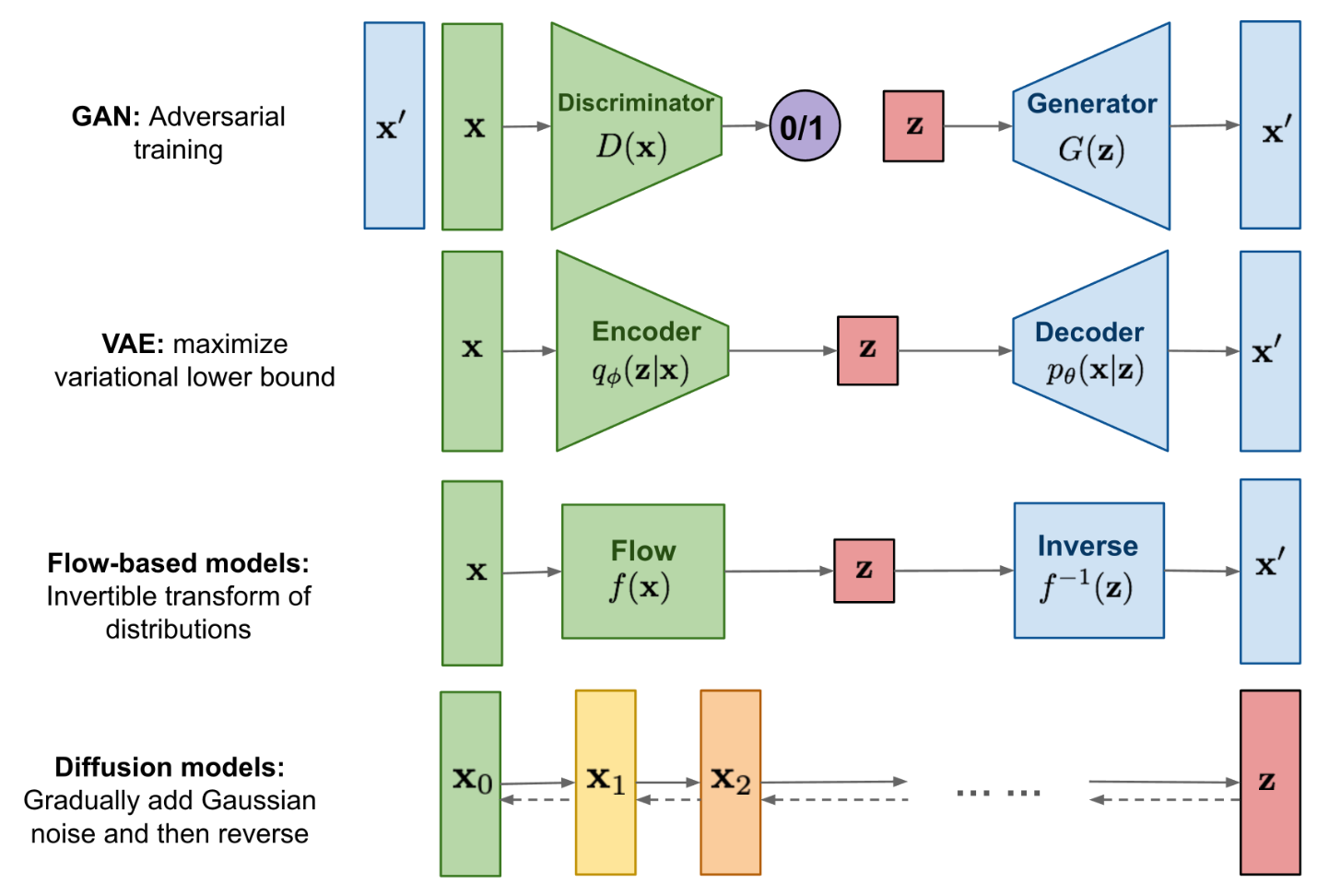
不同生成模型间的关联和区别
-
GAN:生成式对抗网络,使用一个判别器来分类真实样本和生成的样本,另外用一个生成器从噪声出发生成伪样本,两者对抗训练直到判别器无法分辨出真实样本和生成的样本。
-
VAE:变分自编码器,使用一个编码器网络将样本映射到隐层空间,再使用一个解码器将隐层向量重新解码出来。
-
Diffusion Model:包含一个前向过程和反向过程。前向过程从真实样本上不断地加噪音,反向过程从高斯噪音中不断地减噪音,从而生成数据。
本文用到的数学知识
-
贝叶斯公式
\[P(A \mid B)=\frac{P(A) P(B \mid A)}{P(B)}\] -
高斯分布的概率密度函数
\[\mathcal{N}\left(x ; \mu, \sigma^2\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)\] -
两个高斯分布间的KL散度的计算
\[\begin{aligned} & D_{\mathrm{KL}}\left(\mathcal{N}\left(\mu_1, \sigma_1^2\right)|| \mathcal{N}\left(\mu_2, \sigma_2^2\right)\right) \\ =& \int d x\left[\log \mathcal{N}\left(\mu_1, \sigma_1^2\right)-\log \mathcal{N}\left(\mu_2, \sigma_2^2\right)\right] \mathcal{N}\left(\mu_1, \sigma_1^2\right) \\ =& \int d x\left[-\frac{1}{2} \log (2 \pi)-\log \sigma_1-\frac{1}{2}\left(\frac{x-\mu_1}{\sigma_1}\right)^2\right.\left.+\frac{1}{2} \log (2 \pi)+\log \sigma_2+\frac{1}{2}\left(\frac{x-\mu_2}{\sigma_2}\right)^2\right] \\ & \times \frac{1}{\sqrt{2 \pi \sigma_1}} \exp \left[-\frac{1}{2}\left(\frac{x-\mu_1}{\sigma_1}\right)^2\right] \\ =& \mathbb{E}_1 {\left[\log \frac{\sigma_2}{\sigma_1}+\frac{1}{2}\left[\left(\frac{x-\mu_2}{\sigma_2}\right)^2-\left(\frac{x-\mu_1}{\sigma_1}\right)^2\right]\right] } \\ =& \log \frac{\sigma_1}{\sigma_1}+\frac{1}{2 \sigma_2^2} \mathbb{E}_1\left[\left(x-\mu_2\right)^2\right]-\frac{1}{2 \sigma_1^2} \mathbb{E}_1\left[\left(x-\mu_1\right)^2\right] \\ =& \log \frac{\sigma_2}{\sigma_1}+\frac{1}{2 \sigma_2^2} \mathbb{E}_1\left[\left(x-\mu_2\right)^2\right]-\frac{1}{2} \\ =& \log \frac{\sigma_2}{\sigma_1}+\frac{1}{2 \sigma_2^2} \mathbb{E}_1\left[\left(x-\mu_1\right)^2+2\left(x-\mu_1\right)\left(\mu_1-\mu_2\right)+\left(\mu_1-\mu_2\right)^2\right]-\frac{1}{2} \\ =& \log \frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+\left(\mu_1-\mu_2\right)^2}{2 \sigma_2^2}-\frac{1}{2} \end{aligned}\]
扩散模型
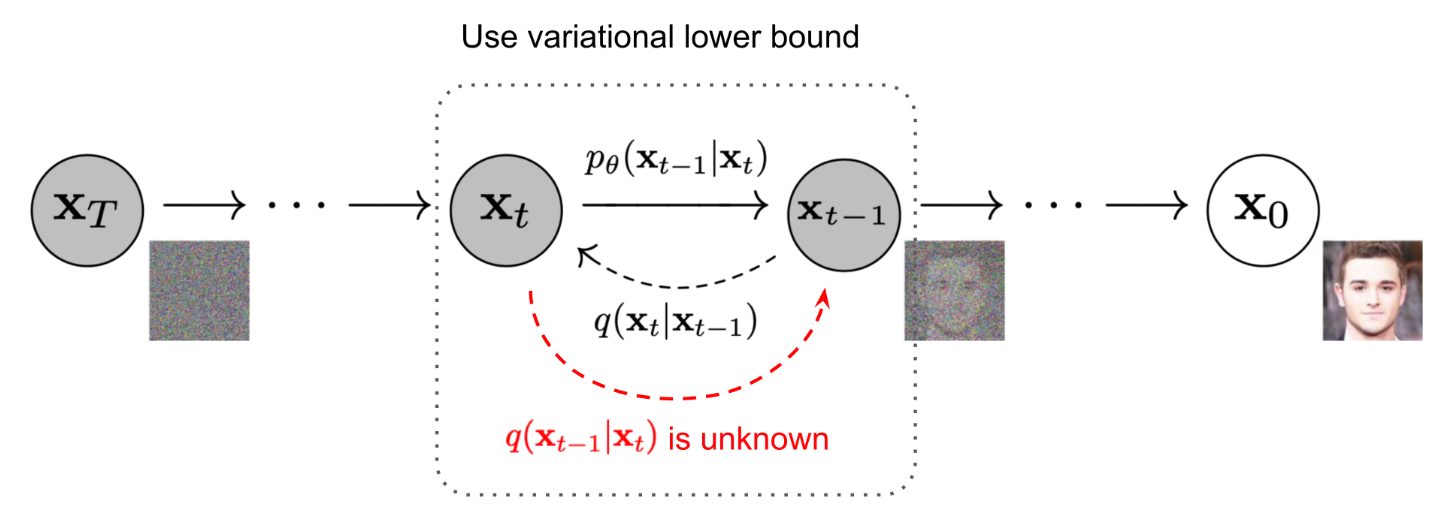
扩散模型包含一个前向过程和一个反向过程。前向过程是在原始样本上不断添加一些高斯噪声,来逐渐破环原本样本的结构,直到变为一个单纯的变量之间互相独立的多元高斯分布。
前向过程
假设我们有一个真实的样本 $\mathbf{x}_{0} \sim q(\mathbf{x})$,前向过程共进行 $T$ 步,每一步添加一些高斯噪声,每一步都可以表示为:
\[q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right) \\ q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)=\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\]其中 $\beta_{t}$ 是一个 $(0, 1)$ 之间的数,它实际上控制了每一步添加的噪声的大小。越大噪声越多,破坏的也就越多;越小噪声越小,保留的也就越多。
在整个前向的过程中,样本 $\mathbf{x}_{0}$ 逐渐失去自己独有的特征,最终退化为一个各向同性的高斯噪声。
上述过程还有一个非常漂亮的性质,那就是我们可以直接采样任意时间 $t$ 的中间表示 $\mathbf{x}_{t}$,而不用迭代地去计算。令 $\alpha_t=1-\beta_t$ 和 $\bar{\alpha}_t=\prod^{t}_{i=1} \alpha_i$,那么我们有
\[\begin{aligned} &\mathbf{x}_t=\sqrt{\alpha_t} \mathbf{x}_{t-1}+\sqrt{1-\alpha_t} \mathbf{z}_{t-1}\\ &=\sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2}+\underbrace{\sqrt{\alpha_t\left(1-\alpha_{t-1}\right)} \mathbf{z}_{t-2}+\sqrt{1-\alpha_t} \mathbf{z}_{t-1}}_{=\sqrt{1-\alpha_t \alpha_{t-1}} \overline{\mathbf{z}}_{t-1}}\\ &=\ldots\\ &=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \overline{\mathbf{z}}_{t-1} \end{aligned}\]其中 $\mathbf{z}_{t-1}, \mathbf{z}_{t-2}, \cdots \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$。
通常来说,前向过程中有 $\beta_1<\beta_2<\ldots<\beta_T$,也就是说破坏力度是越来越大的。相应的有 $\alpha_1>\alpha_2>\ldots>\alpha_T$。
反向过程
如果我们反转上述过程,并从 $q(\mathbf{x}_{t-1} \mid \mathbf{x}_{t})$ 中进行采样,那么就可以从一个高斯噪音 $\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 出发,逐步采样出 $\mathbf{x}_{T-1}, \mathbf{x}_{T-2}, \cdots, \mathbf{x}_1$,最终解码得到数据样本 $\mathbf{x}_{0}=\mathbf{x}$。
如果直接使用贝叶斯公式
\[q \left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=\frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right) q\left(\mathbf{x}_{t-1}\right)}{q\left(\mathbf{x}_t\right)}\]但是我们无法求得 $q(\mathbf{x}_{t-1})$ 和 $q(\mathbf{x}_{t-1})$,因此也无法直接根据前向的过程 $q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)$ 直接求得反向的过程。
但是注意到,如果我们可以给定 $\mathbf{x}_{0}$,在这个条件下使用贝叶斯,那么
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)&=q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right) \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}\\ &\propto \exp \left(-\frac{1}{2}\left(\frac{\left(\mathbf{x}_t-\sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{\beta_t}+\frac{\left(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right)\\ &=\exp \left(-\frac{1}{2}\left(\frac{\mathbf{x}_t^2-2 \sqrt{\alpha_t} \mathbf{x}_t \mathbf{x}_{t-1}+\alpha_t \mathbf{x}_{t-1}^2}{\beta_t}+\frac{\mathbf{x}_{t-1}^2-2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 \mathbf{x}_{t-1}+\bar{\alpha}_{t-1} \mathbf{x}_0^2}{1-\bar{\alpha}_{t-1}}\\ -\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right)\\ &=\exp \left(-\frac{1}{2}\left(\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \mathbf{x}_{t-1}^2-\left(\frac{2 \sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \mathbf{x}_{t-1}+C\left(\mathbf{x}_t, \mathbf{x}_0\right)\right)\right) \end{aligned}\]$C\left(\mathbf{x}_t, \mathbf{x}_0\right)$ 是一些与 $\mathbf{x}_{t-1}$ 无关的项,因此可以忽略。
在上述推导过程中:
- 第二行的第一项用到了
- 第二行的第二项用到了
-
第二行的第三项是将第二项中的 $t-1$ 替换为 $t$ 即可
-
第三行到第四行即为 $a x^2+b x+C=a\left(x+\frac{b}{2 a}\right)^2$
上述的反向的条件高斯分布可以参数化为 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right)$。
高斯分布的方差可以表示为
\[\tilde{\beta}_t=1 /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}\_{t-1}}\right)=1 /\left(\frac{\alpha_t-\bar{\alpha}_t+\beta_t}{\beta_t\left(1-\bar{\alpha}\_{t-1}\right)}\right)=\frac{1-\bar{\alpha}\_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t\]而均值则是
\[\begin{aligned} \tilde{\mu}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) &=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 \\ &=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \cdot \frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} z_t\right) \\ &=\frac{\sqrt{\alpha_t} \cdot \sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{\sqrt{\alpha_t} \cdot\left(1-\bar{\alpha}_t\right)} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \cdot \frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} z_t\right) \\ &=\frac{\alpha_t-\bar{\alpha}_t}{\sqrt{\alpha_t}\left(1-\bar{\alpha}_t\right)} \mathbf{x}_t+\frac{\beta_t}{\left(1-\bar{\alpha}_t\right) \sqrt{\alpha_t}}\left(x_t-\sqrt{1-\bar{\alpha}_t} z_t\right) \\ &=\frac{1-\bar{\alpha}_t}{\sqrt{\alpha_t}\left(1-\bar{\alpha}_t\right)} \mathbf{x}_t-\frac{\beta_t}{\left(1-\bar{\alpha}_t\right) \sqrt{\alpha_t}}\left(\sqrt{1-\bar{\alpha}_t} z_t\right) \\ &=\frac{1}{\sqrt{\alpha_t}} \mathbf{x}_t-\frac{\beta_t}{\sqrt{\left(1-\bar{\alpha}_t\right)} \sqrt{\alpha_t}} z_t \\ &=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{\left(1-\bar{\alpha}_t\right)}} z_t\right) \end{aligned}\]优化目标
如果我们想优化交叉熵,则有
\[\begin{aligned} L_{\mathrm{CE}} &=-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log p_\theta\left(\mathbf{x}_0\right) \\ &=-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log \left(\int p_\theta\left(\mathbf{x}_{0: T}\right) d \mathbf{x}_{1: T}\right) \\ &=-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log \left(\int q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right) \frac{p_\theta\left(\mathbf{x}_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)} d \mathbf{x}_{1: T}\right) \\ &=-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log \left(\mathbb{E}_{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)} \frac{p_\theta\left(\mathbf{x}\_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}\right) \\ & \leq-\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)} \log \frac{p_\theta\left(\mathbf{x}_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)} \\ &=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right]=L_{\mathrm{VLB}} \end{aligned}\]$q_(\mathbf{x}_{0})$ 是真实的数据分布,而 $p_{\theta}(\mathbf{x}_{0})$ 是模型预测的分布。上式中第四行到第五行使用了Jensen不等式的性质 $\log \mathbb{E}[f(x)] \geq \mathbb{E}[\log f(x)]$。
与VAE相似,我们选择使用变分下界来优化负对数似然。该变分下界还可以进一步改写为
\[\begin{aligned} L_{\mathrm{VLB}}&=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right]\\ &=\mathbb{E}_q\left[\log \frac{\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right]\\ &=\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=1}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right]\\ &=\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right]\\ &=\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)} \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\right)+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right]\\ &=\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\\ +\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right]\\ &=\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right]\\ &=\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_T\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\right]\\ &=\mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t=2}^T \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}} \underbrace{-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}] \end{aligned}\]在上述的推导中:
-
第三行到第四行的过程中,将 $t=1$ 的情况从求和中剥离出来
-
第四行到第五行中使用了马尔科夫性质和贝叶斯公式
\[q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)=q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right)=\frac{q\left(\mathbf{x}_t, \mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}=q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\]
将变分下界的每个部分分别标记一下,记作
\[\begin{aligned} L_{\mathrm{VLB}} &=L_T+L_{T-1}+\cdots+L_0 \\ \text { where } L_T &=D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right) \\ L_t &=D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right) \text { for } 1 \leq t \leq T-1 \\ L_0 &=-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) \end{aligned}\]$L_{\mathrm{VLB}}$ 中的每一项(除了$L_{0}$)都是两个高斯分布之间的KL散度,因此他们都是可计算的。$L_{T}$ 是一个常数可以忽略,因为 $q$ 不含可学习的参数,且 $\mathbf{x}_{T}$ 是高斯噪声。
$L_t$ 的参数化
我们的目标是学习一个网络来近似反向过程中的条件分布 $p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \mathbf{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)$,我们需要找一个合适的参数化方式。
-
对于均值 $\mu_\theta\left(x_t, t\right)$ ,我们希望它能够近似真实的反向过程中的分布的均值 $\tilde{\boldsymbol{\mu}}_t=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \mathbf{z}_t\right)$。由于在训练阶段,输入 $\mathbf{x}_{t}$ 是已知的,所以我们选择参数化噪声 $\mathbf{z}_t$,在训练时从 $\mathbf{x}_{t}$ 预测噪声。
-
对于方差 $\Sigma_\theta\left(x_t, t\right)$,DDPM选择将其设置为常数 $\Sigma_\theta\left(x_t, t\right)=\operatorname{diag}\left(\sigma_t^2\right)$。令 $\sigma_t^2=\beta_t \text { or } \sigma_t^2=\tilde{\beta}_t=\frac{1-\bar{\alpha} t-1}{1-\bar{\alpha}_t} \beta_t$。
此时,与 $L_t$ 有关的两个高斯分布分别为
\[q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\mu}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} z_t\right), \tilde{\Sigma}_t=\bar{\beta}_t \mathbf{I}\right)\] \[p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \mu_\theta\left(\mathbf{x}_t, t\right)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} z_\theta\left(\mathbf{x}_t, t\right)\right), \Sigma_\theta\left(\mathbf{x}_t, t\right)=\sigma_t^2 \mathbf{I}\right)\]那么 $L_t$ 的计算方式为
\[\begin{aligned} L_t &= D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right) \\&=\mathbb{E}_{\mathbf{x}_0, \mathbf{z}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right\|_2^2}\left\|\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ &=\mathbb{E}_{\mathbf{x}_0, \mathbf{z}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \mathbf{z}_t\right)-\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \mathbf{z}_\theta\left(\mathbf{x}_t, t\right)\right)\right\|^2\right] \\ &=\mathbb{E}_{\mathbf{x}_0, \mathbf{z}}\left[\frac{\beta_t^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\mathbf{z}_t-\mathbf{z}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ &=\mathbb{E}_{\mathbf{x}_0, \mathbf{z}}\left[\frac{\beta_t^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\mathbf{z}_t-\mathbf{z}_\theta\left(\sqrt{\bar{\alpha}_t \mathbf{x}_0}+\sqrt{1-\bar{\alpha}_t} \mathbf{z}_t, t\right)\right\|^2\right] \end{aligned}\]所以本质上,$L_t$ 在优化两个高斯噪音 $\mathbf{z}_t$ 和 $\mathbf{z}_{\theta}$ 之间的MSE损失。
上述的MSE损失在实际训练中不稳定,因此 DDPM采用了如下简化版的损失函数
\[L_t^{\text {simple }}=\mathbb{E}_{\mathbf{x}_0, \mathbf{z}_t}\left[\left\|\mathbf{z}_t-\mathbf{z}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \mathbf{z}_t, t\right)\right\|^2\right]\]整体的训练和采样
