代码已开源：https://github.com/yuleiniu/cfvqa/

背景与动机

    VQA（视觉问答）系统以一张图片和一个关于这张图片形式自由、开放式的自然语言问题作为输入，以生成一条自然语言答案作为输出。它是视觉对话、视觉阅读理解和多模态推理等任务的基础。

    A VQA system takes as input an image and a free-form, open-ended, natural-language question about the image and produces a natural-language answer as the output.

    但是近期的研究表明，VQA模型可能依赖于虚假的语言关联，而不是多模态推理。例如，回答如“Do you see a…”这类问题时，回答“yes”即可在VQA v1.0数据集中取得90%的准确率。如果 VQA 模型仅仅记住训练数据中的强语言先验，它就无法很好地泛化，特别是在最近提出的 VQA-CP 数据集上，其中先验在训练和测试集中有很大的不同。

解决思路

核心问题是：如何在有偏的训练下完成无偏的推理。

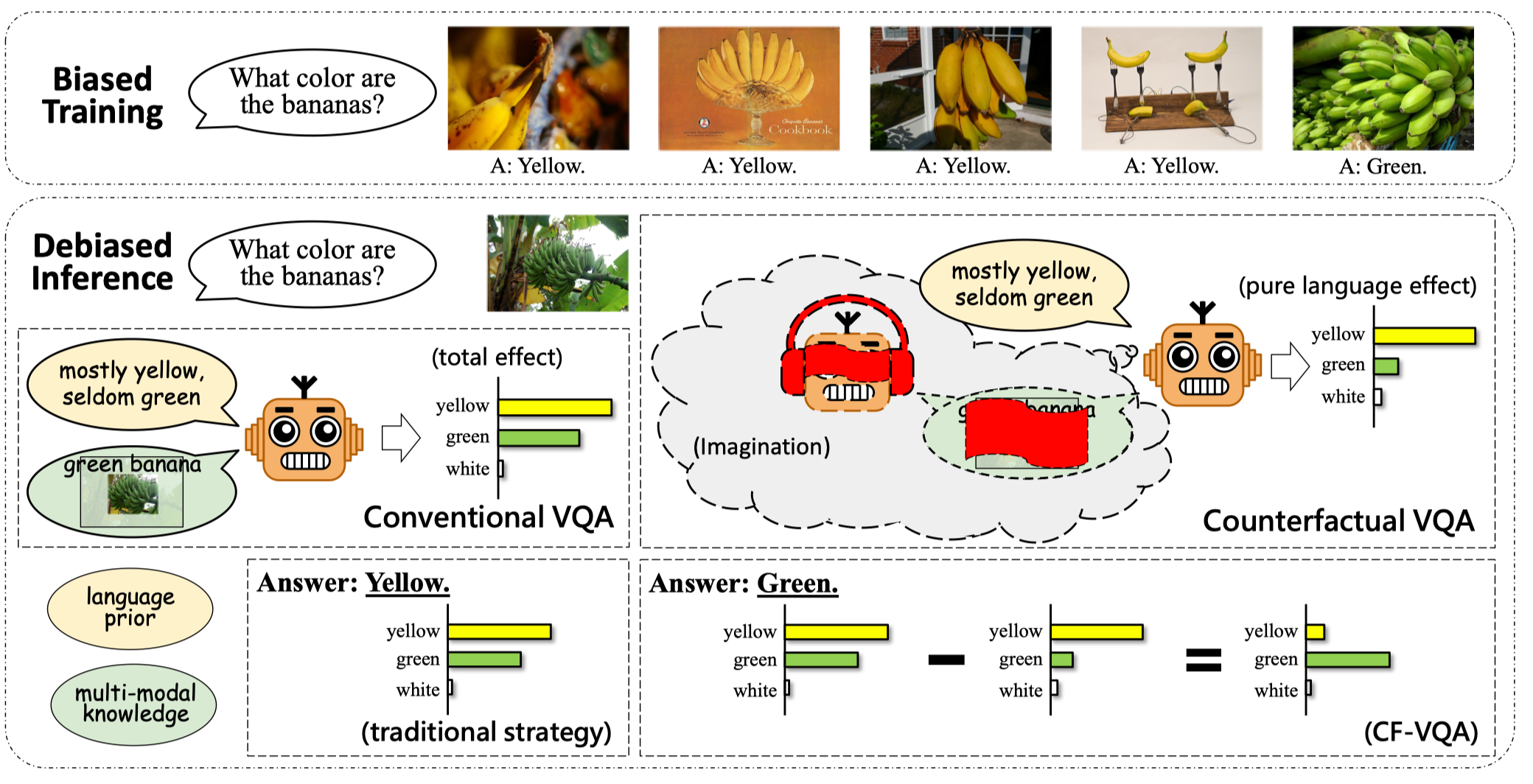
    作者提出了一个新的反事实推理框架，称作CF-VQA，来减少VQA中的语言偏差。总的来说，作者将语言偏差建模为问题对答案的直接因果效应。如下图所示，作者引入了两种场景，分别是传统的VQA和反事实的VQA，来分别评估总因果效应和直接语言效应。

• 传统的VQA：如果机器听到了问题Q，看见了图像V，然后提取了多模态知识K，那么回答A会是什么样？

• 反事实VQA：如果机器听到了问题Q，但是没有提取K或者看到V，答案会是什么样的？

    传统的VQA描述的场景是，Q和V都是可见的，在此基础上估计V和Q对A的总因果效应。然而，传统的VQA不能解耦单模态语言关联和多模态推理，例如直接和间接因果效应。考虑如下的反事实问题：如果机器没有进行反事实推理会怎么样。也就是，当机器听到了问题Q，但是多模态推理的能力被阻隔，VQA模型只能依赖于单模态的影响。此时，语言的偏差可以认为是Q对A的直接因果效应。因此，在作者提出的VQA推理框架中，按照语言先验的方法进行训练，在测试阶段，从总因果效应中减去纯语言效应，即可得到无偏的因果效应。

因果推断背景知识

为了帮助读者理解，作者在文中介绍了所需的因果推断的背景知识。

    对于上图这样的因果图，在事实场景下，有 $m=M_x=M(X=x)$ 。在反事实场景下，$X$ 可以被设置为对于$M$ 和 $Y$ 不同的值。例如，$Y_{x,M_{x^*}}$ 描述的是当 $X$ 被设置为 $x$ 且 $M$ 被设置为当 $X$ 为 $x^*$ 时 $Y$ 的取值 $Y_{x,M_{x^*}}=Y(X=x,M=M(X=x^*))$。

假设 $ X=x $ 代表执行某种处理，$ X=x^{*} $ 代表不执行该种处理，X对Y的总因果效应（Total Effect，TE）记为：

    总因果效应可以分解为自然直接效应（Natural Direct Effect，NDE）和总间接效应（Total Indirect Effect，TIE）。即 $TE=NDE+TIE$。NDE表示当中介变量M被阻断（M被设置为 $X=x^*$ 时的取值），$X$ 从 $x^*$ 变为 $x$ 时 $Y$ 的增长。

TIE是TE与NDE的差值，即：

因果视角下的VQA

    在掌握上述的因果推断基础知识后，详细介绍作者的具体做法。

任务定义

VQA本质上是一个多类别分类任务，VQA系统的任务是，给定一个图片 $V=v$ 和一个问题 $Q=q$ ，从候选集合 $\mathcal{A}={a}$ 选择一个合适的答案。

问题建模

    VQA任务的因果图如下所示，V和Q对于A的因果效应可以分为单模态效应和多模态效应。单模态效应就是V或者Q对于A的直接效应$V \rightarrow A$ 或者 $Q\rightarrow A$。而多模态效应是V和Q通过多模态知识K对答案A的间接效应 $V,Q \rightarrow K \rightarrow A$。作者认为应该排除纯语言效应 $Q\rightarrow A$ 来减少VQA中的语言偏差。

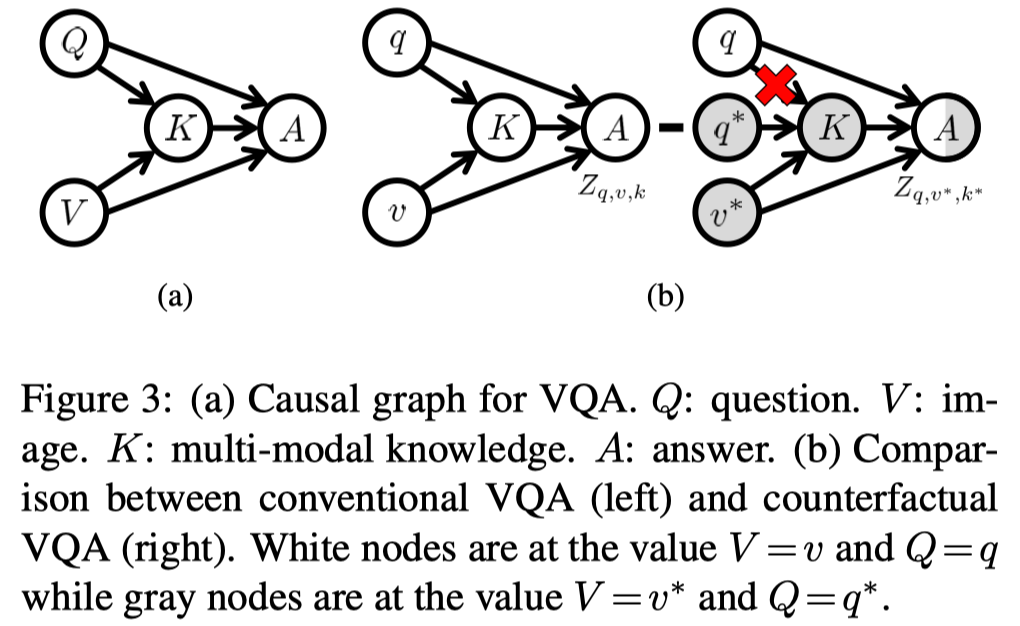
    那么根据上文提到的因果推断框架中的标记，当 $V$ 为 $v$，$Q$ 为 $q$ 时，答案 $a$ 的分数为：

不失一般性，忽略 $a$，即得到 $Y_{v,q}=Y(V=v,Q=q)$。相似的，$K$ 的反事实标记为 $K_{v,q}=K(V=v,Q=q)$。

    从上面的因果图可以看出，有三条路径直接指向 $A$，即 $Q \rightarrow A$、$V \rightarrow A$ 和 $K \rightarrow A$。因此，可以将 $Y_{v,q}$ 重写为Q、V和K的函数：

根据上一部分因果效应的定义，$V=v, Q=q$ 对于 $A=a$ 的总因果效应可以记为

    正如在背景部分所介绍的，VQA模型通常面临着虚假关联的问题，因此无法有效的执行多模态推理。因此，作者想要使得VQA模型去除问题的直接影响。

    为了达到这个目标，作者提出反事实的VQA，通过阻断 $K$ 和 $V$ 来衡量 $Q=q$ 对 $A=a$ 的因果效应。反事实VQA描述的场景是， $Q=q$ ，而 $K$ 保持为 $k^*$（$Q=q^*,V=v^*$ 时$K$ 的取值）。由于中介变量 $K$ 对于输入的回复被阻断，模型只能依赖于给定的问题做决定。

    上图中的（b）展示了传统的VQA和反事实VQA的比较。通过反事实VQA减去无任何处理下的场景，便可以得到问题$Q$ 对于答案$A$ 的自然直接效应NDE

    由于 $Q$ 对于中介变量 $K$ 的效应被阻断，NDE显式地刻画了语言偏差。因此，从总的因果效应中减去语言偏差，便可以实现语言的去偏：

在测试阶段时，选择有着最大TIE的作为最终的答案，这与之前基于后验概率$p(a \mid v,q)$ 的传统策略是完全不同的。

CF-VQA的具体实现

模型实现

    上述公式中的 $Z_{q,v,k}$ 可以使用三个神经网络 $\mathcal{F}_{Q}$、$\mathcal{F}_{V}$ 和 $\mathcal{F}_{VQ}$ 和一个聚合函数 $h$ 来表示：

其中 $\mathcal{F}_{Q}$ 表示仅语言的分支 $Q \rightarrow A$ ，$\mathcal{F}_{V}$ 表示仅视觉的分支 $V \rightarrow A$ ，$V,Q \rightarrow A$ 表示视觉-语言分支 $V,Q \rightarrow K \rightarrow A$。而最终输出的分数 $Z_{q,v,k}$ 由函数 $h$ 聚合得到。

    根据前面的介绍，无任何处理的场景是阻断了从视觉或者语言传递的信号，即没有给定问题或者图片。然而神经网络并不能处理输入是空值的情况，因此，作者假设在无处理时，神经网络会给出等概率的分值。在这种情况下，$Z_{q}$、$Z_{v}$ 和 $Z_{k}$ 可以被表示为：

其中，$c$ 代表一个常数。作者解释说，在这里使用均匀分布的原因有二：

1. 对于人类来说，如果完全不知道问题的类型或者话题，那么随机猜测答案将是很自然的想法。

2. 由于使用 $z_{v}^{*}$ 和 $z_{q}^{*}$ 来估计 $Q$ 的NDE，均匀分布可以保证一个安全稳定的估计。

聚合策略

关于 $h$ 函数的聚合策略，作者提出了两种非线性的聚合策略，Harmonic(HM)和SUM：

其中 $Z_{\mathrm{HM}}=\sigma\left(Z_{q}\right) \cdot \sigma\left(Z_{v}\right) \cdot \sigma\left(Z_{k}\right)。$

其中 $Z_{\mathrm{SUM}}=Z_{q}+Z_{v}+Z_{k}$。

训练和推断

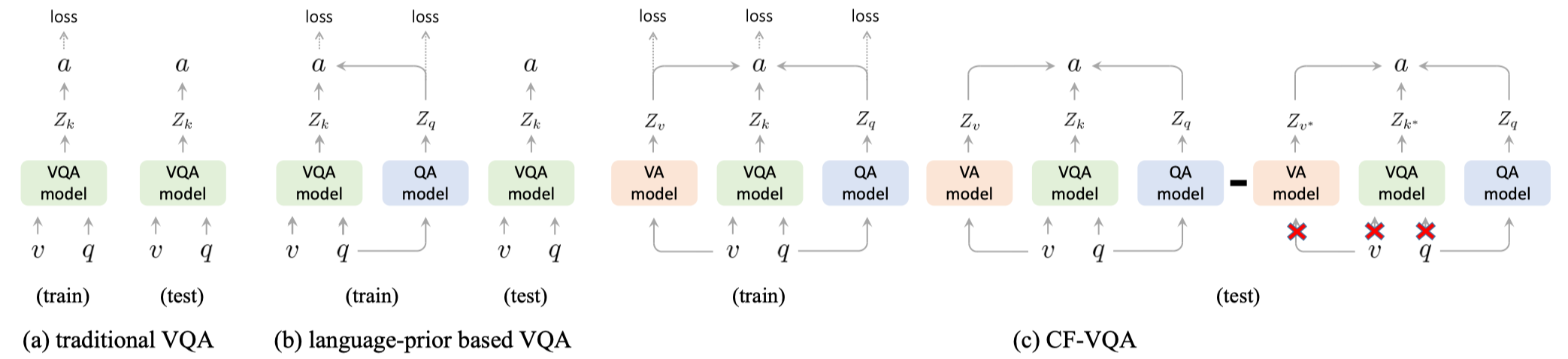
如上图所示，给定三元组$(v,q,a)$ 之后，可以通过优化分数 $Z_{q,v,k}$、 $Z_{q}$ 和 $Z_{v}$ 的交叉熵损失来训练模型：

除此之外，还有一个可学习的常数 $c$，它控制了 $Z_{q,v,k}$ 分布的锐度，类似于softmax中的温度系数。作者假设NDE的锐度应该与TE类似，不然会导致TIE的训练受到TE或者NDE的主导。因此作者引入了一个KL散度项来估计 $c$：

其中，$p(a \mid q, v, k)=\operatorname{softmax}\left(Z_{q, v, k}\right)$ ，$p(a \mid q, v^*, k^*)=\operatorname{softmax}\left(Z_{q, v^*, k^*}\right)$。在最小化 $\mathcal{L}_{k l}$ 时只更新 $c$ 。

    最终的损失函数是：

在执行推断时，无偏的因果效应实现是：

• Previous
  论文笔记
• Next
  论文笔记